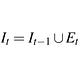Understanding Why Analysis
Reflections on the course
Intro
The purpose of this document is to reflect on my experience taking real analysis as an undergraduate economics major (not a math double major.) It could perhaps provide some insight into what went well, what didn't go well, and my expectation versus reality on the difficulty and the content.
Preparation
I took real analysis (RA) when I was a senior, it was the first upper division math class I had taken, as I was not majoring or minoring in math. The class had reached a sort of mythical level in the undergraduate economics student's ethos who is interested in graduate school. A prohibitively difficult hurdle. That was certainly the case for me, but after the course actually started, it became clear that this course is like any other, preparing for it will pay dividends.
Taking Discrete Mathematics First
The best preparation for me was to take what's called "Discrete Mathematics" at my university. It's essentially an introduction to logic and proofs (with some probability sprinkled at the end, though it was of no use to RA specifically.) It teaches you fundamental proof writing techniques (Direct proofs, Contradiction, Contrapositive, Induction) which build off of an understanding of logical operators and rules (e.g. DeMorgan's Law.) With this, you are also taught some essential set theory knowledge, in fact, I think about 90% of what I know about set theory now comes from Discrete Math, as RA applies set theory constantly, but the vast majority of it was covered in my case in Discrete Math.
Discrete Math gives you tools and understanding so you can actually focus on the content of RA without getting caught up in how certain rules of logic work, how to write a proof, and getting mixed up with set operations. I can confidently say that I would have struggled much more without having prior exposure to these concepts.
Additional Materials
If you are unable to take such a course before you take RA, there are many books that serve the same purpose. One that helped me immensely was "How to Prove it: A Structured Approach". For the course itself, we used: "Discrete Mathematics and its Applications", which was also fantastic. Additionally, you can also just pick up a RA book before the course starts. In the book "Understanding Analysis", by Abbot, the first chapter goes over these preliminaries (in less detail than you would otherwise get in a different book, but still.)
For any additional preparation, MIT has a full course online which includes recorded lectures, HW, and exams. I didn't fully make use of this, but It was useful in doing some review to see a different perspective on how to approach the same problems.
Purpose: Not an "IQ Test"
Something that I heard often before taking the class is that it's just an "IQ Test." Implying that the material in the course has nothing to do with what you would be learning in an econ PhD program, and that you generally don't get much out of the class other than as a signaling tool.
However, I feel like this is not the case. RA is not some mysterious or particularly niche topic. It's calculus, which people tend to accept ubiquitously as necessary for studying economics or doing economics research. RA is nothing more than what you learned in calculus I-III, at a more rigorous level. If you already believe a solid foundation in calculus is necessary for econ, but view RA as just a signaling litmus test, RA is nothing but calculus.
My limited knowledge of PhD level courses in economics suggest that calculus and knowing how to write proofs are necessary for performing well. Regardless of if you want to be a theorist or not, you have to take the core theory classes.
Mathematical Familiarity
But beyond just understanding calculus at a better level and learning how to write proofs, there is a lot of utility in RA.
During the semester I took the course, I was also taking a class in probability, a class in advanced econometrics (Econ 143 at UC Berkeley), and writing an honors thesis. Each of these, I found useful applications of what I learned in RA for.
More than the fact that both of the classes I was taking uses calculus, I was also just much more comfortable with reading and understanding math. This came from having more exposure to notation, with reading and writing proofs, and set theory. This is also likely because RA was my first upper-division math class, if I had taken abstract algebra or a proof based linear algebra class first, I likely would have received the same benefits from those courses.
This same comfortability was useful in reading econ papers, and not being put-off by notation (or, intimidated, honestly.)
Taking RA with these classes was also useful for perspective on each of them. RA is all about proving calculus, probability has many applications of calculus, and econometrics has applications of probability. A rough, but helpful landscape in my mind of the gradient from pure to applied math.
Notes on Typesetting and GitHub
For my courses that semester, I committed to typing my homework and problem sets in LaTeX. Before, I just took pictures of my work and uploaded them. It's a rather uncomfortable transition, but I'm glad I chose to do so. It was a good excuse to become more comfortable with LaTeX, and it acted as a final review of everything before submitting it, as I had to essentially rewrite all of my work again. I used overleaf, which I highly recommend. I has git integration, which I'm currently using to create a solutions document for the 4th edition linear algebra done right. It's good practice to get comfortable with working on multiple remote repositories with git, which of course is also an essential skill.
Conclusion
I hope this short note was helpful to someone preparing to take the class, and/or wondering what the actual material is like and how it could be useful in potential applications to econ research from my limited perspective.